카지노에서 돈을 딸 수 있는 완벽한 전략
과연 페어플레이일까?
어느새 프랑크 주변은 인파로 우글거린다. 과감한 이론들이 속삭임에 실려 오고간다. 딜러가 속임수를 쓰는 것일까? 룰렛 기구에 문제가 있는 것일까? 프랑크는 돌처럼 굳어진 표정으로 자신의 칩을 응시한다. 마침내 그는 1만 240유로어치의 칩 더미를 검은색 구역에 밀어놓는다. 이것마저 잃으면 프랑크는 빈털터리가 되고 만다!
“자, 이제 자네가 야심차게 개발한 백전백승의 전략을 보여주게나, 프랑크.”
R SS R S RRR SSSS RR SS R S R SSSSS RRRRRRRRRRR S RR SSS R SS R SSS R S RRRR SSS RRR S R S RR SSSSS RRRR S RRR S RRR SS R SS RRR S RR SS RR S R S
카지노에 들어서자마자 친구 빌이 만사 제쳐놓고 재촉한다. 프랑크는 룰렛에서 거의 확실하게 돈을 따는 방법을 안다. 그는 일관되게 검은색 칸에 돈을 걸고, 구슬이 빨간색 칸으로 떨어지면 판돈을 두 배로 올릴 전략을 세웠다. 이를테면 목표 금액이 5유로라면, 검은색 칸에 5유로를 건다. 운 좋게 구슬이 검은색 칸에 떨어지면 목표를 달성하지만 빨간색 칸에 떨어지더라도 그다음 판에 10유로를 걸면 된다. 왜냐하면 두 번째 판에 그가 이겨서 20유로를 받으면 두 번째 판까지 걸었던 15유로를 감안했을 때 결국 5유로를 딴 셈이 되기 때문이다. 열두 번 연속으로 구슬이 빨간색 칸으로 떨어질 확률은 0이나 다름없다고 확신한 프랑크는 정확히 열두 번 게임할 수 있는 2만 475유로를 준비해서 실전에 임한다.
“3, 루즈(빨간색), 앵페르(홀수), 망크(18 이하의 숫자)!”
“34, 루즈, 페르(짝수), 파세(19 이상의 숫자)!”
“3, 루즈, 앵페르, 망크!”
연거푸 열한 번 빨간색이다! 어느새 프랑크 주변은 인파로 우글거린다. 과감한 이론들이 속삭임에 실려 오고간다. 딜러가 속임수를 쓰는 것일까? 룰렛 기구에 문제가 있는 것일까? 프랑크는 돌처럼 굳어진 표정으로 자신의 칩을 응시한다. 마침내 그는 1만 240유로어치의 칩 더미를 검은색 구역에 밀어놓는다. 이것마저 잃으면 프랑크는 빈털터리가 되고 만다!
도박꾼들의 어리석은 추론
믿기 어렵겠지만, 위의 이야기에 제시된 숫자들은 다음과 같이 2007년 3월 10일에 호엔쥐부르크 카지노에서 실제로 나온 것들이다(R : 빨간색, S : 검은색).
위의 열이 ‘무작위하지 않다고’ 여길 통계학자는 아무도 없을 것이다. 이 열에는 R이 54개, S가 46개 들어 있다. 이 비율은 상식적으로 기대되는 비율 50 : 50에 가깝다.
그렇지만 프랑크의 도박이 대실패로 끝난 것은 개연성이 상당히 낮은 사건이다. 프랑크가 채택한 백전백승의 전략은 99.95퍼센트 성공하게 되어 있다. 그러나 안타깝게도 확률만 계산하는 것으로는 충분하지 않다. 도박은 돈이 걸린 놀이이고, 따라서 결과 각각의 확률뿐 아니라 그 결과에 동반된 손익이 얼마나 큰지도 따져야 한다.
이른바 기댓값은 이런 맥락에서 유용한 수학 개념이다. 기댓값은 도박이 ‘공정한지’ 여부를 알려준다. 기댓값이 0보다 작다는 것은, 장기적으로 손님이 돈을 잃고 카지노가 돈을 번다는 뜻이다. 그리고 룰렛에서는 베팅을 어떻게 하든 상관없이 기댓값은 0보다 작다.

기댓값(E)이란, 가능한 사건들이 n개 있다면 그것들 각각의 확률 p와 이익 q를 곱해서 전부 더했을 때 나오는 값이다.  프랑크가 한 룰렛 11판에서 나올 수 있는 결과들(빨간색과 검은색의 배열들)은 211=2048개, 그중 2047개의 결과들에는 검은색이 적어도 1개 들어 있으므로 프랑크가 5유로를 딴다. 반대로 단 1개의 불운한 결과가 발생하면 그는 1만 235유로를 잃는다. 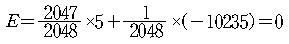 기댓값이 0이라는 것은 게임이 공정하다는 뜻이다. 그러나 게임이 공정하다면 카지노는 돈을 벌지 못할 것이다. 카지노는 기댓값이 0보다 작게 하기 위해 무언가를 장치했다! | ||


- 수학 시트콤 크리스토프 드뢰서 저/전대호 역/이우일 그림 | 해나무
이 책은 공식을 발견하거나 이론을 정립한 수학자 이야기나 수학의 역사가 아니더라도 얼마든지 흥미진진하고 솔깃한 스토리텔링형 수학이 가능하다는 것을 보여준다. TV 드라마나 시트콤을 볼 때처럼 자신도 주인공과 함께 고민하게 하는 책이다. 소금물의 농도나 주사위의 확률 따위가 아닌 우리가 살아가면서 정말 궁금한 것들을 한 편 한 편의 실감나는 이야기로 재구성한다…
‘대한민국 No.1 문화웹진’ 예스24 채널예스


-
글 | 크리스토프 드뢰서 Christoph Drosser
독일의 주간지 《디 차이트 Die Zeit》의 과학 담당 편집자로, 1997년부터 일상적인 속설에 관한 과학 칼럼 <맞아요? Stimmt’s?>를 연재했다. 이 칼럼은 책으로도 엮여 좋은 반응을 얻었으며, 현재 독일의 공영방송사 NDR의 라디오 프로그램으로 방송되고 있다. 드뢰서는 일상 속 수학을 다룬 《수학 시트콤 Der Mathematikverfuhrer》으로 독일에서 수학 신드롬을 일으켰으며, 2008년에 독일수학협회로부터 언론인상을 수상했다.
저서로는 《질문을 쏟아놓는 방법 Wie fragt man Locher in den Bauch?》 《무한도전 신비한 수학탐험 Wie groß ist unendlich?》 《일기예보, 믿을까 말까? Das Lexikon der Wetterirrtumer》(예르크 카헬만 공저) 《치마가 짧아지면, 경제는 성장한다 : 현대의 미신들 Wenn die Rocke kurzer werden, wachst die Wirtschaft. Die besten modernen Legenden》 《음악을 아세요? Hast du Tone?》 등이 있다.
-
-
수학 시트콤
<크리스토프 드뢰서> 저/<전대호> 역/<이우일> 그림15,300원(10%
 + 5%
+ 5% )
)
독일의 유명한 과학 칼럼니스트인 저자 크리스토프 드뢰서는 《수학 시트콤(원제 : Der Mathematikverf?hrer)》에서 드라마 같은 설정으로 우리의 시선을 사로잡고는 그 속에서 생각지도 못한 수학을 이끌어낸다. 원래 수학의 기초는 일상에서 비롯된 것! 수많은 수학 공식은 과거 언젠가 실용적인 문제들을 ..
PYCHYESWEB03


































 + 5%
+ 5% )
)